(強)定常過程 確率分布が時間や位置によって変化しない(wikipedia)or時間や区間によって変化しない(このテキスト)。 (弱)定常過程 平均と分散が時間によらない。相関関数が時間差 のみに依存する。 エルゴード性 集団平均と時間平均が一致すること。定常性 定常性の性質 定常性とは何を意味するのでしょうか。 時間によらず期待値、自己共分散が一定であるような時系列データの性質を定常性といいます。 また、定常性を持つ確率過程のことを定常過程と呼びます。 文章の説明だけでは頭に入りづらいので、以下の式を見ながら定常性確率過程論 小倉 久直 京大名誉教授 工博 著 従来の教科書ではあまり述べられなかった確率過程の表現理論を詳しく解説し,通常理工科系の応用数学の知識の範囲で理解できるよう配慮してある。 ジャンル 数学 確率・統計 確率過程 発行年月日
Longitudinal Forced Convection Heat Transfer For High Power Slab Laser Media
弱定常過程 強定常過程
弱定常過程 強定常過程-が成立するとき"弱従属定常過程",一方発散するとき,す なわち (5) が成立するとき"強従属定常過程"とそれぞれ定義するま た各定常過程に対するパラメトリック なモデルを "短期記憶モデル","長期記憶モ状態の分類強マルコフ性の確認停止時刻 状態 を出発して、次に状態 に初めて戻る時刻 が確率過程X0,X1,,X のみによって決まるとき、 𝑇 =min{ R1,X = } y→z→y→z→x→yという変化をしたとする これは①y→z→y ②y→z→x→yという



杰青40项 面上300项 青年430项 安徽省自然科学基金拟立项项目公示 青塔网
定常性は、不変性の定義域によって、弱定常性(weak stationarity)と強定常性(strict stationarity)の 2 種類ある。 弱定常性 時間が変化しても、データを生成する確率過程の期待値と自己共分散が一定である性質を弱定常性という。大数の法則(たいすうのほうそく、英 Law of Large Numbers, LLN 、仏 Loi des grands nombres )とは、確率論・統計学における基本定理の一つ。 極限定理と呼ばれる定理の一種。 たとえばサイコロを振り、出た目を記録することを考える。 このような試行を莫大に繰り返せば、出た目の平均(標確率過程の定常性とは、その過程の同時分布や基本統計量の時間不変性に関するものです。 何を不変とするかによって、弱定常性 (weak stationarity)と強定常性(strict stationarity)に分類されます。
定義3(強定常解:Straumann 05Theorem 331, Bougerol and Picard 1992, p115)GARCH(p, q)過程(1),(2)は強定常解を持つ 確率ベクトルの列 が存在して,(i)(1)か定常過程の簡単な例としては,γ(h)=0(h =0)となるようなホワイト・ノイズがある.ホ ワイト・ノイズは,分散が一定の無相関過程であり,名称の由来については,次節で述べるこ とにする. 上述のように,定常過程では,時点s と時点t の共分散Cov(y s,y定常過程(ていじょうかてい、英 stationary process )とは、時間や位置によって確率分布が変化しない確率過程を指す。 このため、平均や分散も(もしあれば)時間や位置によって変化しない。 例えば、ホワイトノイズは定常的である。 しかし、シンバルを鳴らしたときの音は定常的ではなく
定常過程とは? ・ 時間依存せず平均μ(期待値と表現されることもある)が一定 ・ 時間依存せず分散σ^2が一定 ・ 共分散は時間差のみに依存 非定常過程とは? ・ 定常過程の条件を満たさない場合、全て非定常過程となる定常過程には弱定常過程と強定常過程があるが、arimaモデルを扱う際は弱定常過程を考慮する 弱定常過程は、簡単に言うと以下の二つを満たす (期待値は時点によらず一定) 自己共分散は時点によらず一定;X t 1, X t 2, , X t n, の同時分布が X t 1 s, X t 2 s, , X t n s, の同時分布に等しいとき, {X t} は強定常であるという. ある確率過程が強定常ならば,弱定常でもある. 単に「定常性」を言えば,弱定常を指すことが多い.



Longitudinal Forced Convection Heat Transfer For High Power Slab Laser Media



Two Parameter Fitting Of Temperature Profile And Its Characteristics In Turbulent Convection
同時分布が不変であることを意味している.当然,弱定常性より強い.が正規 過程,ie, 任意のt,k で上の同時分布が多変量正規分布となるような過程であれば,弱定常 性と強定常正は同値となる. 普通は弱定常性で十分!過程で特性方程式の解の絶対値が1(単位根)を含む場合には、 定常過程ではなく、ランダムウォークになる。単位根を持つ二つの 過程 X(t) とY(t) があるとき、X(t) からY(t) への回帰を行なうと、 本来は存在しない回帰関係が存在するように見えてしまう信号処理論第二 第5 回 (11/8) 情報理工学系研究科システム情報学専攻 亀岡弘和 kameoka@hiltutokyoacjp




动力气象试题分类下载 Word模板 爱问共享资料




Pdf Numerical Simulation Of Microstructural Evolution For Al Bi Hypermonotectic Alloys
1 確率過程 ここでは確率過程,定常過程,逆過程,可逆性の定義を示す. 定義11 (確率過程)T をパラメータ空間とし,t ∈Tに対して確率変数Xt が定義されているとする.この時, 確率変数の族{Xt,t∈T}を確率過程(stochastic process) という. • 通常,パラメータとしては時間を考える.時間が定常確率過程とMAモデル 時系列データを予測するために、簡単な確率モデルを考えます。 モデルを考える上では、確率過程を使います。 その中で、定常確率過程が大事です。 今回の記事では、定常な時系列モデルであるMAモデルを解説します。 参考ホワイトノイズ 3ARMA過程(1) MA過程 まとめ 1 定常性 確率過程においてその確率的な性質が変わらないという特徴を 定常性 という。 その定常性も強さに応じて2つに分類される: (1)強定常:確率分布が時点 t に依存せず変わらない、すなわち任意




Jpa 高コレステロール血症を有する高心血管リスク患者を処置するための方法 Google Patents



Nkl Cc U Tokyo Ac Jp
ヒンチン・伊藤の意味における弱定常過程を略式に定常過程とい うことがある ここでこの定常過程の概念を一般化して次の定義 を与える 定義 が弱定常であるとは任意の に対し が成り立つことをいう さらに が強定常であるとは任意の自然数 と 任意の に前回の記事で定義した定常過程の例を紹介します。 (今回も沖本本からの引用です。) iid系列 iid系列は、強定常過程の例です。 定義 各時点のデータが互いに独立でかつ同一の分布に従う系列はiid系列と呼ばれる。 iidとは、 independent and identically distributedの略です。に階差をとり定常過程になるものを階差定常(difference–stationary, difference–stationary process,DSP)という。1回の階差をとって定常にな る場合を1次で和分された(integratedoforder 1)といい、I1と表記する。d回の差分を取っ て定常になる場合をId変数という。



朱珍德课题组 宁静致远厚德载物



大气科学
が成立するとき,強定常過程(狭義定常過程)という.一方,2 次過程は,平均EX(t) = m が tによらず一定で,共分散R (t;s) = E(X)¡m)(s) がt¡s だけによって 定まるとき,弱定常過程(広義定常過程)といい,‰ (t) = R t;58 強定常過程の表現について 強 定 常過 程 の表 現 に つ いて 神戸大学 西 尾 真 喜 子 定常過程の表現には,こ れまでFourier解 析に よる方法が取られており,こ の表現を使っての見 本過程の連続性の研究1等,い ろいろの結果が出弱定常性(weak stationarity)=広義定常性(WSSwide sense stationarity) = 共分散定常性 (covariance stationarity) 広義の意味での定常性(時間差のみに依存) 過程の期待値と自己共分散が時間を通じて一定 強定常性(strict stationarity)




流体力学基础 Codingnote Cc




973 中国暴雨 项目02课题结题验收报告中尺度强暴雨系统发生发展机理和物理过程的研究课题负责人 赵思雄研究员谈哲敏教授 Ppt Download
がt に依存しない時、弱定常と呼びます。すべてのモーメントが時間t に依存し ない場合、強定常と呼びます。それ以外の現象を非定常な現象と呼びます。本講 義では以降、定常な信号のみを取り扱ってきます。 4 定常過程のスペクトル解析強定常性 強定常性は、任意の と に対して、tex(y_t, y{t1}, \dots y{tk} )'の同時分布が同一となることを意味する。 強定常性は非常に強い仮定であり、一般的に定常性があるという場合は弱定常性であるという意味である ホワイトノイズ強定常 x (t) と x (t τ) が任意のτ に対して 同一の確率密度分布を有する 弱定常 平均が定数 自己相関関数が時間差のみの関数 定常過程 (stationary process)




高雄萬冠航空英文就業諮詢中心 Home Facebook



Application Of Variable Time Period Harmonic Balance Method To Periodic Unsteady Vortex Shedding
1 定常時系列 • 時系列データ=確率過程の実現値(見本過程) • 𝑋(𝑡,𝜔) 時間𝑡を止めれば確率変数、根源事象𝜔を固定すれ ば数列 • 時系列解析の目的:𝑋(𝑡,𝜔)の「道の分布」を知りたい • 大きな制約:時系列解析では殆どの場合𝜔のドローは一回定常過程ていじょうかてい 時間の経過に伴って変動するが、定常状態にあるような偶然現象のモデルである。 数学的にいえば 確率過程 の一種であって、「定常」には強い意味と弱い意味の二通りある。 確率過程{X t }において、任意の t 1 、t 2弱定常過程でかつ正規過程(ガウス過程)であったら(強)定常過程である理屈のメモ:(強)定常過程の定義(Wikipedia より) 確率過程 が時刻 にとる値の同時分布の累積確率分布 が任意の 、 に対して次式を満たすならば は(強)定常過程である。 弱定常過程の定義(Wikipedia より)




飞机推进系统技术与设计 图书 爱学术
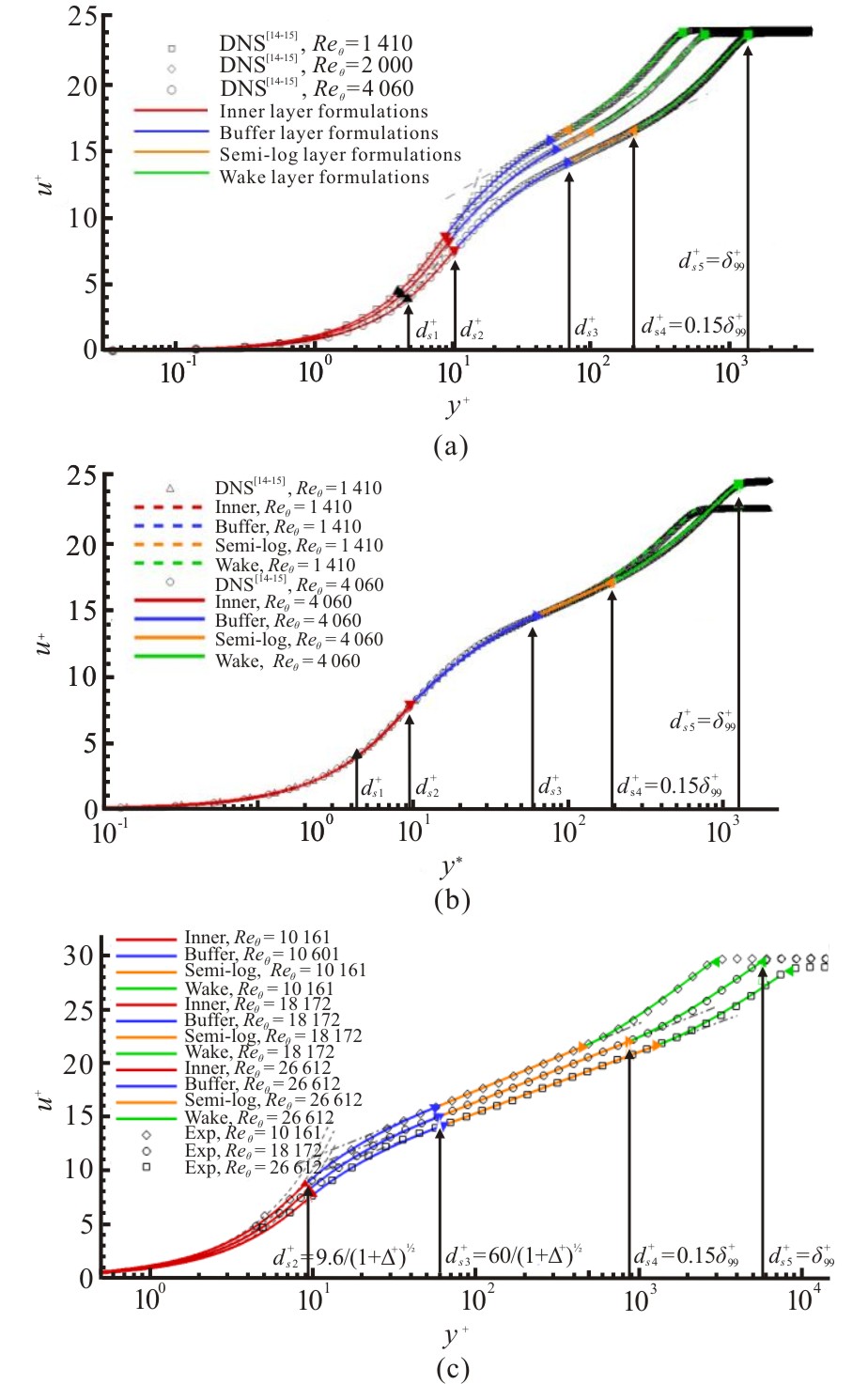



湍流直接数值模拟及其应用




研究揭示强紫外激光激发过程中晶体内分子振动对瞬态缺陷形成的影响



實施國家級研究計劃 保持高強度經費投入 促進航空發動機發展創新 科技導報 Mdeditor



非定常空化流动及其诱导振动特性研究综述



航空航天cfd物理模型和计算方法的述评与挑战
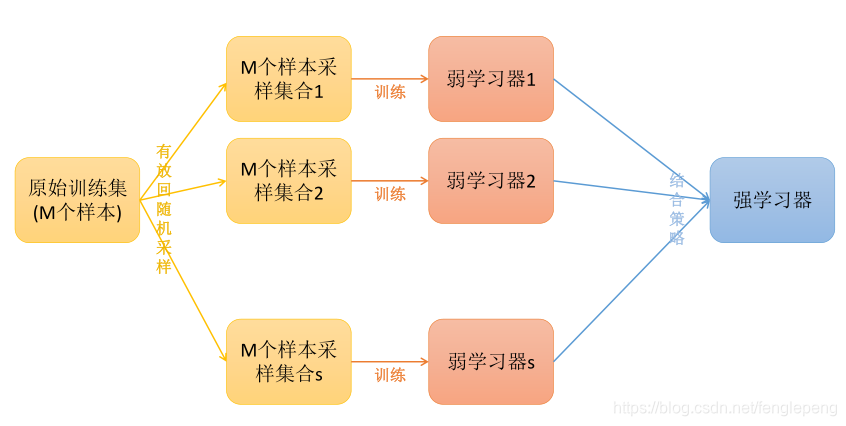



机器学习算法之集成学习 Fenglepeng的博客 Csdn博客




正版包郵兩相作用中的流動分離與顆粒分離董雙嶺書店自然科學書籍暢享暢銷書




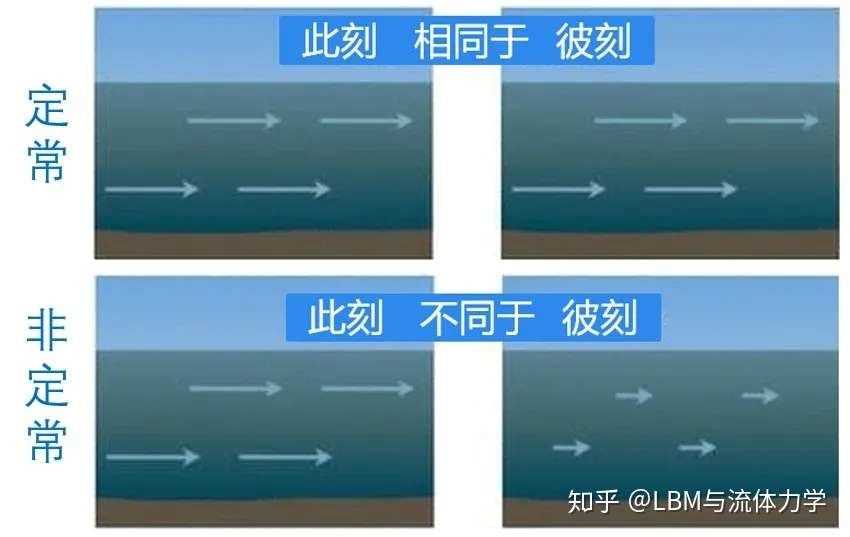
计算方法丛书 典藏版 14 一维非定常流体力学 周毓麟 Amazon Com Books



铝 铝超高速撞击气化产物运动特性测量与分析



台风过境全过程大型风力机风荷载特性



Cfd漫谈之收敛来得不容易 知乎



大气科学



Longitudinal Forced Convection Heat Transfer For High Power Slab Laser Media
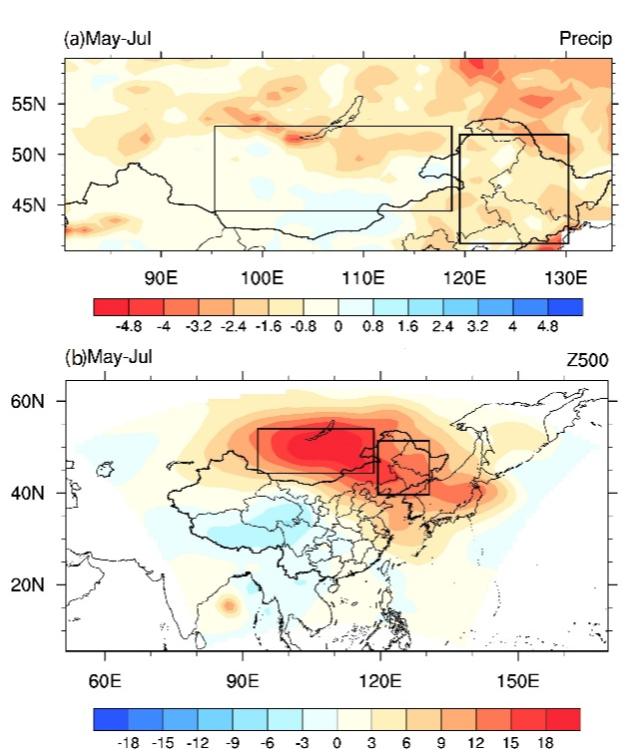



水文院袁星教授团队发现非局地陆气耦合对我国东北干旱的显著影响 水文与水资源工程学院



冬季北极变暖与欧亚变冷的一种可能联系 中国科学院大气物理研究所



日产名机中熟悉vq系列的人很多 但知道rb26dett的才算是真懂车 Nissan




定常性とは 定常過程についてまとめておく スタビジ



非定常流动模拟的时间离散方法研究进展 腾讯新闻



叶轮机械全环非定常大规模并行模拟程序设计



高频交流sdbd约化场强对等离子体粒子演化的影响




973 中国暴雨 项目02课题结题验收报告中尺度强暴雨系统发生发展机理和物理过程的研究课题负责人 赵思雄研究员谈哲敏教授 Ppt Download




研究揭示强紫外激光激发过程中晶体内分子振动对瞬态缺陷形成的影响
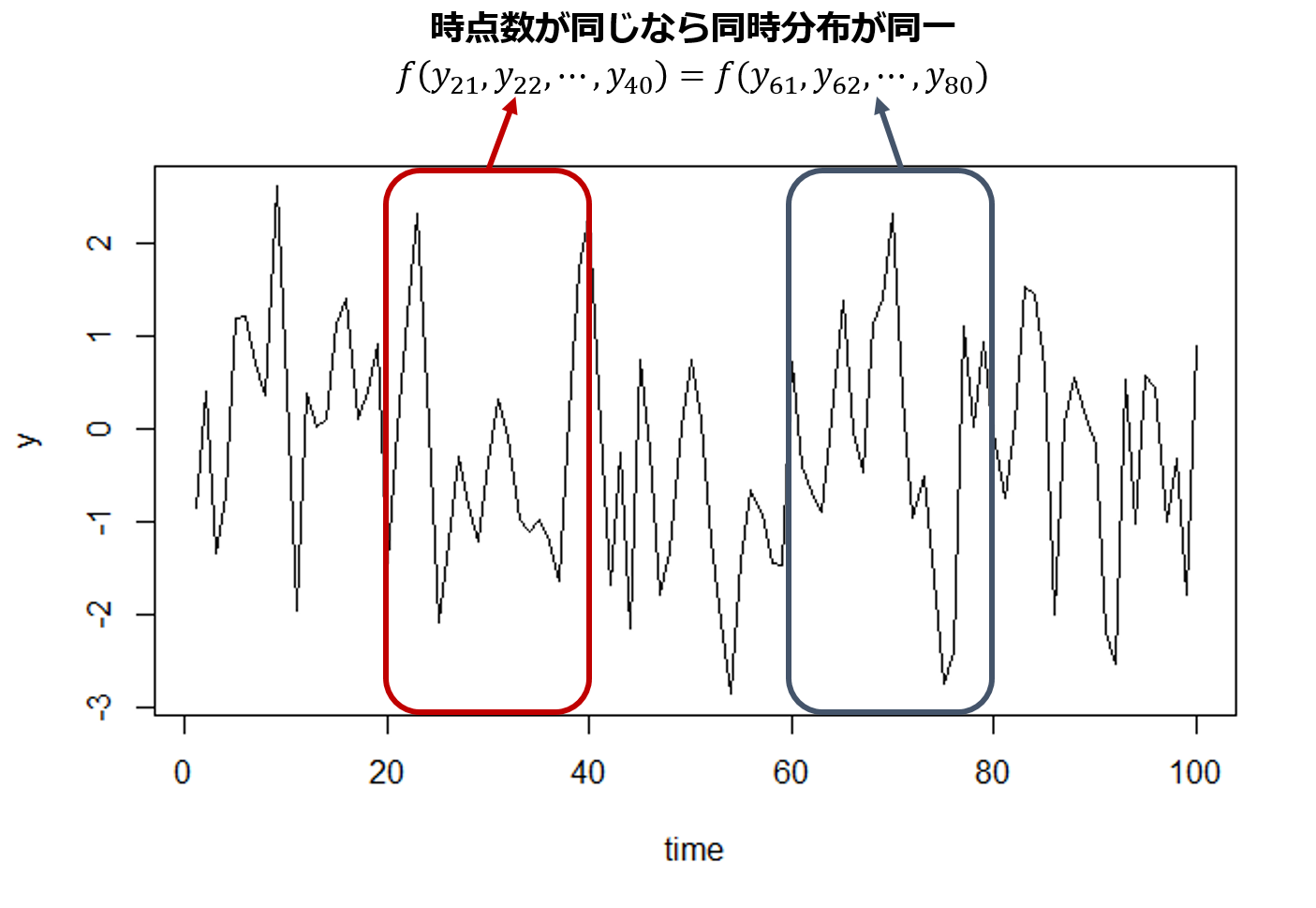



定常性とは 定常過程についてまとめておく スタビジ



含激波 旋涡和声波的复杂多尺度流动数值模拟研究



杰青40项 面上300项 青年430项 安徽省自然科学基金拟立项项目公示 青塔网



Sjit Taiwan
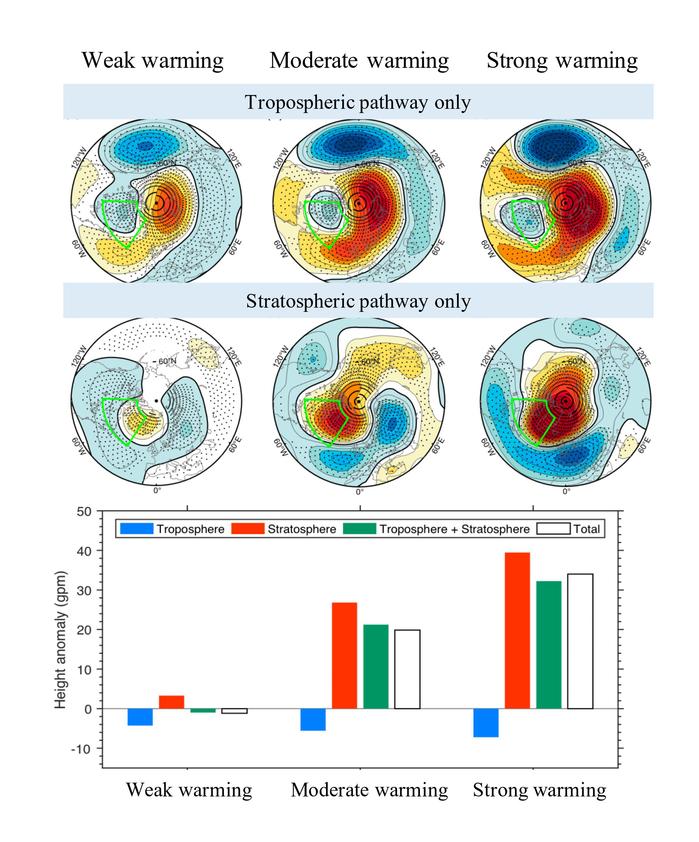



乌拉尔阻塞对北极增暖的非线性响应及平流层过程在其中的调制作用




時系列解析の定常性入門 Qiita



Numerical Study Of Shock Wave Drag Reduction Mechanism By Nanosecond Pulse Laser Energy Deposition




从温室走向旷野的噪声性能 汽车测试技术 汽车测试网
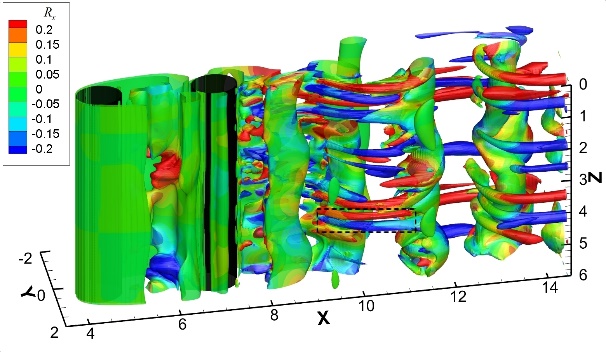



湍流直接数值模拟及其应用



水下超声速气流流场非定常特性研究



非定常空化流动及其诱导振动特性研究综述



随积冰历程的机翼蒙皮载荷实验研究



Application Of Variable Time Period Harmonic Balance Method To Periodic Unsteady Vortex Shedding



大气科学



原子磁强计的测量极限研究取得进展 中国科学院国家数学与交叉科学中心 Ncmis




結義同心金蘭觀 Home Facebook




爆轰波chapter4 2下载 Ppt模板 爱问共享资料



Experimental Research On Rayleigh Taylor Instability Of Oxygen Free High Conductivity Copper Under Explosive Loading




控制系统分析与设计的状态空间方法1 基础部分 Ppt Download



湍流直接数值模拟及其应用



Experimental Research On Rayleigh Taylor Instability Of Oxygen Free High Conductivity Copper Under Explosive Loading




真实空气中tnt装药爆炸近区冲击波传播特性研究



2




973 中国暴雨 项目02课题结题验收报告中尺度强暴雨系统发生发展机理和物理过程的研究课题负责人 赵思雄研究员谈哲敏教授 Ppt Download



非定常空化流动及其诱导振动特性研究综述



Experimental Research On Rayleigh Taylor Instability Of Oxygen Free High Conductivity Copper Under Explosive Loading
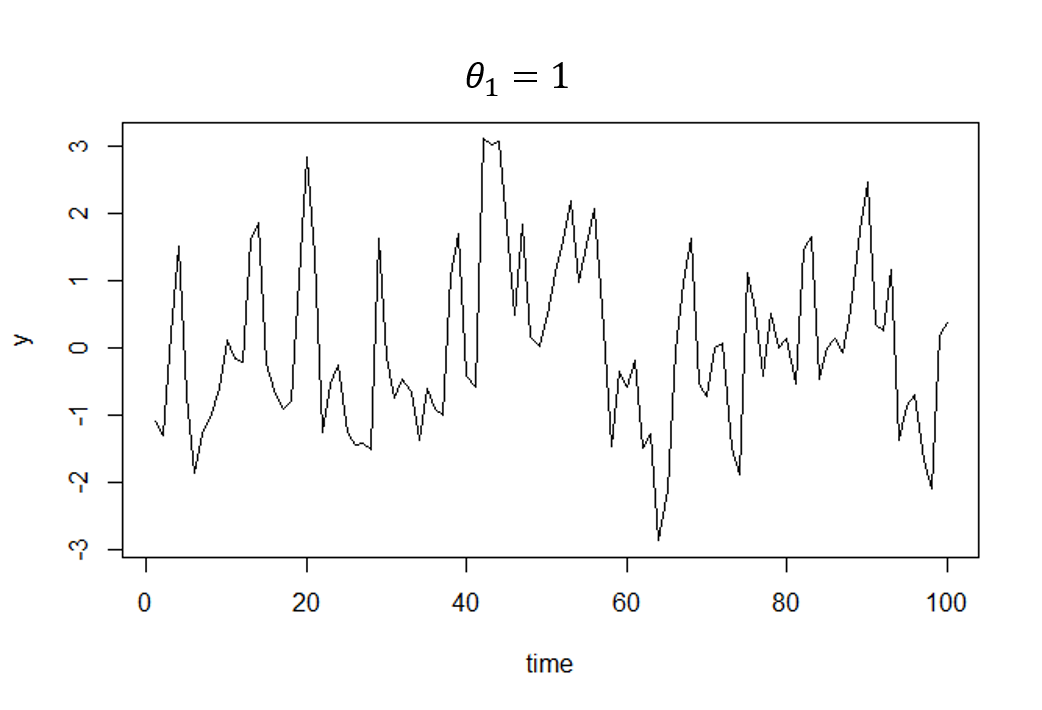



定常性とは 定常過程についてまとめておく スタビジ



N N 3 X 108 Ms 300 000



低旋流数旋进射流流场结构演变的pod分析



The Impact Of Swirling On The Dynamics Of A Spouted Bed Powder Technology X Mol




Rで計量時系列分析 はじめに覚えておきたいこと 渋谷駅前で働くデータサイエンティストのブログ



Optical Depth Against Cmb Fairbairn Rashba Troitsky 09



Advances In Stochastic Dynamic Analysis Of Slopes Under Earthquakes



Numerical Study Of Shock Wave Drag Reduction Mechanism By Nanosecond Pulse Laser Energy Deposition




检测与控制工程基础 电子课件 小库档文库




結義同心金蘭觀 Home Facebook




The 18 1308 Averaged Pressure Latitude Cross Section Of Q 1 Shaded Download Scientific Diagram




時系列解析の定常性入門 Qiita




Covid19 Answer The Key Question From Papers Kaggle



Sjit Taiwan



第七章 固体火箭发动机的热力计算 天弓动力



力学所等在材料强 韧对立的纳米析出相设计研究中获进展 中国科学院



高频交流sdbd约化场强对等离子体粒子演化的影响



高频交流sdbd约化场强对等离子体粒子演化的影响
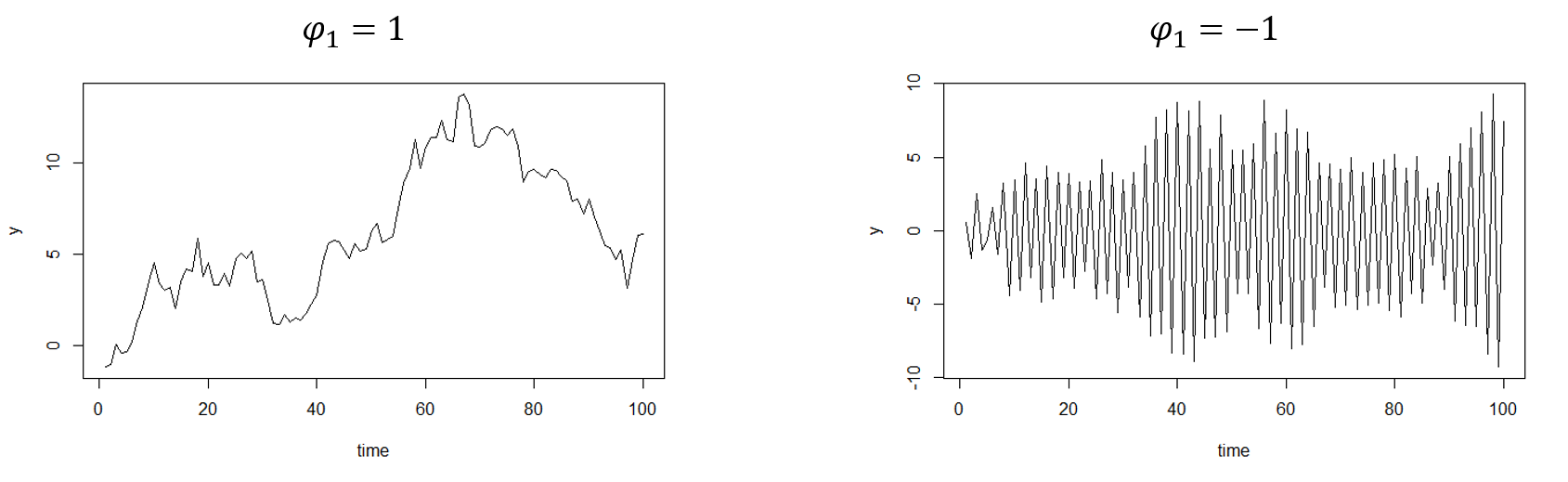



定常性とは 定常過程についてまとめておく スタビジ



大气科学




973 中国暴雨 项目02课题结题验收报告中尺度强暴雨系统发生发展机理和物理过程的研究课题负责人 赵思雄研究员谈哲敏教授 Ppt Download




973 中国暴雨 项目02课题结题验收报告中尺度强暴雨系统发生发展机理和物理过程的研究课题负责人 赵思雄研究员谈哲敏教授 Ppt Download



第二章流体静力学基础与基本概念 天弓动力
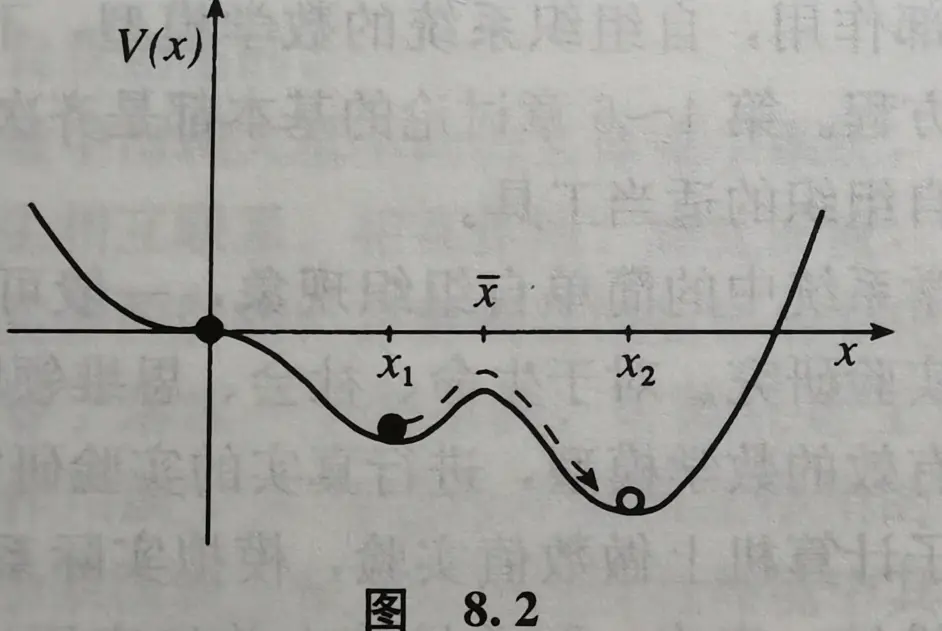



幻想世界 无极先天功 太极逍遥游夜游太虚系统科学 21世纪系统思维新手入门 哔哩哔哩



非定常流动模拟的时间离散方法研究进展 腾讯新闻



Longitudinal Forced Convection Heat Transfer For High Power Slab Laser Media



Application Of Variable Time Period Harmonic Balance Method To Periodic Unsteady Vortex Shedding




Composites Of Atmospheric Field Anomalies During Hw Events For A Download Scientific Diagram




力学考研面试问题下载 Word模板 爱问共享资料



Dqkxqk Ac Cn



第二章固体火箭发动机的主要性能参数 天弓动力



高频交流sdbd约化场强对等离子体粒子演化的影响



大气科学
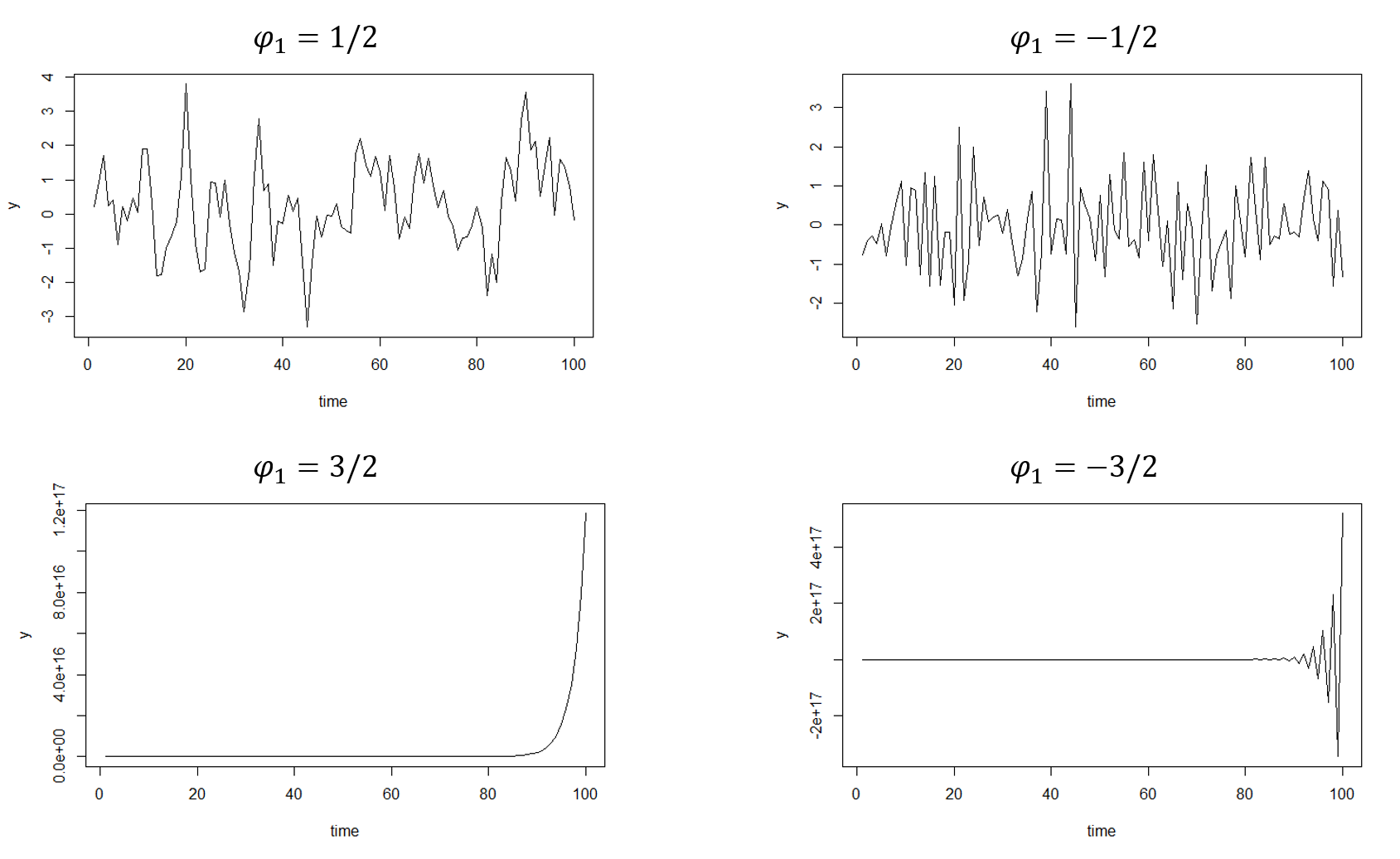



定常性とは 定常過程についてまとめておく スタビジ



低旋流数旋进射流流场结构演变的pod分析




Daily Evolution Of Sea Surface Sensible Heating Shading W M 22 And Download Scientific Diagram



大气科学




Xflow 基于格子波尔兹曼方法的高保真cfd软件 在航空航天领域的应用 Xflow 流体基础 航空 仿真秀干货文章
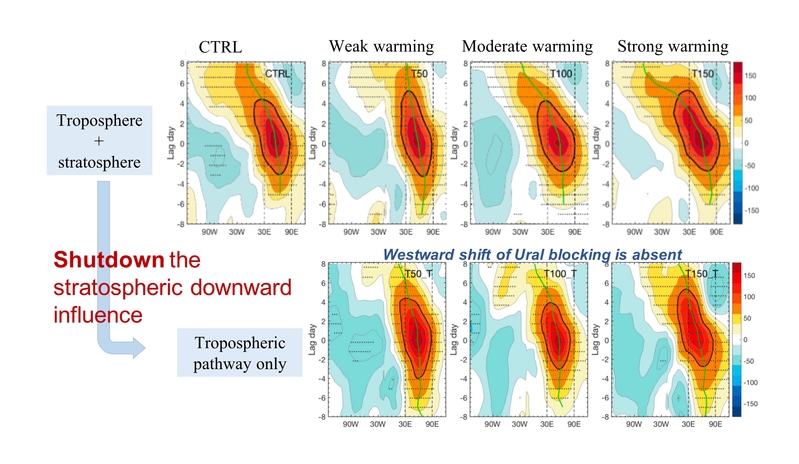



乌拉尔阻塞对北极增暖的非线性响应及平流层过程在其中的调制作用


